W Rozporządzeniu w sprawie sposobu opracowywania sprawozdania z wysokości średnich wynagrodzeń nauczycieli […] w części zatytułowanej „Objaśnienia” do „wzoru sprawozdania z wysokości średnich wynagrodzeń […] stanowi się: „[…] Wszystkie dane oraz wyniki obliczeń powinny być wpisane z dokładnością do dwóch miejsc po przecinku. Obliczenia powinny zostać wykonane na danych z taką samą dokładnością.”.

(1) „Objaśnienia” są jednostką redakcyjną załącznika do rozporządzenia definiującego „wzór sprawozdania”.

(2) Zacytowane dwa zdania wyżej utwierdzają w przekonaniu, że nadużywany w art. 30a i w przywołanym rozporządzeniu zwrot „ustalić” (w różnych odmianach gramatycznych) należy rozumieć jako „obliczyć”.

(3) W związku z pkt (1) zacytowane dwa zdania wyżej obowiązują do danych i obliczeń dotyczących „wzoru sprawozdania”.

(4) …nie dotyczą zatem wszystkich danych i obliczeń w odniesieniu do rozumienia słów „przeprowadzić analizę wydatków poniesionych na wynagrodzenia”.

(5) Treści zawarte w „Objaśnieniach” przekraczają zakresy wynikające ze „wzoru sprawozdania”, co oznacza, że pkt (4) staje się co najmniej dyskusyjny (rzecz jednak nie jest rozstrzygalna i staje się uznaniowym elementem przyjętej metodologii liczenia).

(6) Dane „powinny być” wpisywane oraz obliczenia „powinny zostać wykonane” „z dokładnością do dwóch miejsc po przecinku” – żaden z cytowanych zwrotów nie determinuje twierdzenia, że należy stosować najpowszechniejszą standardową (szkolną) metodę zaokrąglania wyników obliczeń „do dwóch miejsc po przecinku” (w szczególności tylko dlatego, że jest najpowszechniejsza, bo jest powszechnie nauczana w polskiej szkole).

(7) Czyli wybór metody zaokrąglania wyników obliczeń „do dwóch miejsc po przecinku” staje się kolejnym uznaniowym elementem przyjętej metodologii liczenia. A metod zaokrąglania jest kilka…

Która wartość jest poprawna w zawartym poniżej przykładzie?

Dane zawarte w przykładzie zdarzyły się gdzieś w Polsce. „Dyskusja” pomiędzy Kontrolowanym a Kontrolującym także się zdarzyła. Zapowiedź: wyjdzie z końcem tego tekstu, że owa „dyskusja” była (w najłagodniejszym ujęciu) stratą czasu dla Kontrolowanego i Kontrolującego.

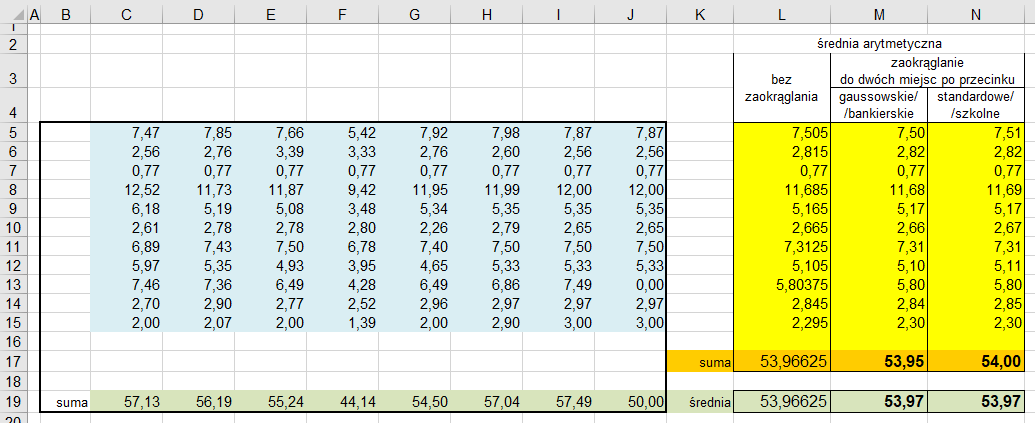
Obszar z niebieskim tłem (umówmy się, że to jest „niebieski” – i podobnie co do pozostałych tu wskazywanych barw) zawiera dane do dalszych obliczeń (są to miesięczne struktury zatrudnienia z 11 podmiotów prawa oświatowego w jednej z grup awansu zawodowego. Tuż poniżej obszaru z danymi na zielonym tle znajdują się sumy dla każdego z ośmiu miesięcy.

Po prawej stronie (obszar z żółtym tłem) wyliczono dla każdego z podmiotów średnią arytmetyczną. W kolumnie [L] – bez zaokrąglania; w kolumnie [M] – zastosowano zaokrąglanie do dwóch miejsc po przecinku z użyciem metody zwanej gaussowską (bankierską – w zasobach internetowych można znaleźć bardzo dużo treści dotyczących tej metody i zasadności jej stosowania); w kolumnie [N] – zastosowano zaokrąglanie z użyciem metody zwanej standardową (szkolną).

W tym samym żółtym obszarze (ciemniejsza żółta barwa tła) policzono sumę – czyli „średnioroczną liczbę etatów nauczycieli”. Alternatywnie poniżej (zielone tło) policzono także te same wartości, ale nie w wyniku sumowania średnich, lecz poprzez policzenie średnich z uzyskanych wcześniej sum.

Ostatecznie – w zależności od przyjętej (i całkowicie tu dopuszczalnej) metodologii liczenia i zaokrąglania otrzymano trzy wyniki: 53,95; 54,00; 53,97. Który z nich jest poprawny? Odpowiedź może być zaskakująca, bo brzmi – żaden! Poprawny wynik to 53,96625. Gdyby jednak zadać pytanie nieco inaczej: który wynik jest „zgodny z prawem”? Odpowiedź: 53,95; 54,00; 53,97 – każdy z nich jest równie „zgodny z prawem”; żeby to „zrozumieć” proszę wrócić do początku tego tekstu.

Ach, przepraszam – chyba źle napisałem. Tego nie trzeba „rozumieć”. Proszę przyjąć za „prawdę obiektywną” rzecz następującą: „Proszę nie liczyć poprawnie, bo będzie źle. Proszę policzyć zgodnie z prawem, to będzie dobrze.”. A w tym tu konkretnym przypadku „dobrze” oznacza: 53,95; ale także 54,00 i nawet 53,97. W pewnym pojmowaniu sprawy (tego wątku tu nie rozwijam) swego rodzaju najlepszym wynikiem będzie tu ten, który najlepiej wspiera „interes” jednostki samorządu terytorialnego. Ale z innej perspektywy lepszym to będzie ten, który jest bardziej w „interesie” nauczycieli. I dość łatwo jest wskazać, który w jakiej perspektywie jest „lepszy”.

Jeżeli zatem Czytelniku tak sparametryzujesz narzędzia wspomagania tych obliczeń, że ci na przykład w takim przypadku, jak ten tu wyżej, wyjdzie 53,95 a Kontrolujący Cię sprawdzi i wyliczy sobie 54,00 – to kto tu będzie miał rację. Ciągle jeszcze w bardzo wielu miejscach się twierdzi, że Kontrolujący. A dlaczego? Bo tak, bo to twierdzi Kontrolujący. Zauważam jednak jak jednocześnie bardzo to się w minionych kilku latach zmienia (przynajmniej jeśli chodzi o obowiązki wynikające z art. 30a) – Kontrolujący już naprawdę wiedzą z czym tu mają do czynienia i wiedzą także, że dyskusja, który w danym tu przykładzie wynik jest dobry (uwaga – ma być dobry, czyli zgodny z prawem, a nie poprawny) jest po prostu stratą czasu (w najłagodniejszym ujęciu).

A gdyby jeszcze zauważyć, że dane (te na niebieskim tle) także przecież są wynikiem obliczeń z przyjętą metodologią zaokrąglania…

Zalecane narzędzia pozwalają uzyskać wynik „najlepszy” dla danej perspektywy pojmowania – o ile kogokolwiek będzie tu interesować przeprowadzanie analizy w różnych perspektywach pojmowania.

Domyślnie – narzędzia wspomagania przeprowadzania analizy funkcjonują w sposób dający wyniki „zgodne z prawem” te możliwie najbardziej bliskie wartościom poprawnym – (statystycznie) najczęściej. I żeby sobie głowy nie zawracać – proszę po prostu tych narzędzi użyć i będzie dobrze. A „dyskusje” z Kontrolującymi - o ile może być prawdą, że się zdarzają - no, każdy sobie radzi tak, jak radzić sobie umie.

Krzysztof Sługocki, 13.08.2020