Dlaczego wyliczona w analizie różnica – [1] na załączonym niżej rysunku – (przy założeniu, że jest ujemna) nie jest zwykle równa (wtedy co do znaku traktowana jako dodatnia) sumie wyliczonych do wypłacenia jednorazowych dodatków uzupełniających ([2] na rysunku)?

Ujemna różnica [1] (…z rozporządzenia w sprawie sposobu opracowywania sprawozdania: „Kwotę różnicy należy obliczyć […] jako różnicę wydatków poniesionych na wynagrodzenia […] i sumy iloczynów średniorocznej liczby etatów i średnich wynagrodzeń, o których mowa w art. 30 ust. 3 Karty Nauczyciela […]. Liczba ujemna informuje o kwocie różnicy, jaką należy podzielić i wypłacić w formie jednorazowych dodatków uzupełniających.”) jest dzielona na jednorazowe dodatki uzupełniające [4]. Art. 30a ust. 3: „Kwota różnicy, o której mowa w ust. 2, jest dzielona między nauczycieli […] i wypłacana […] w formie jednorazowego dodatku uzupełniającego ustalanego proporcjonalnie do okresu zatrudnienia oraz osobistej stawki wynagrodzenia zasadniczego nauczyciela […]”.

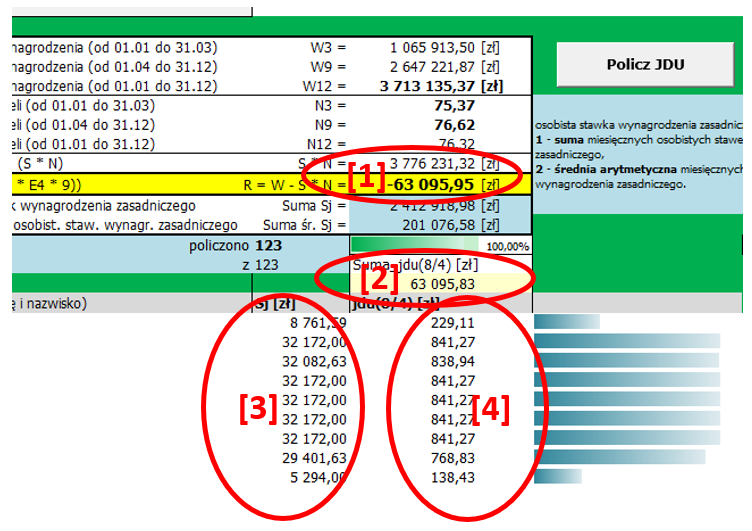
Osobista stawka wynagrodzenia zasadniczego [3]: „Dla każdego nauczyciela oddzielnie należy wyliczyć osobistą stawkę wynagrodzenia zasadniczego proporcjonalnie do okresu zatrudnienia według następującego wzoru: Sj = A x B x C […]” – więc wyliczanie jednorazowego dodatku uzupełniającego proporcjonalnie do osobistej stawki wynagrodzenia zasadniczego [3] będzie także proporcjonalnym do okresu zatrudnienia…
Czyli liczby oznaczone znakiem [3] to są właśnie wyliczone dla każdego nauczyciela oddzielnie „osobiste stawki wynagrodzenia zasadniczego”; różnica [1] została podzielona na jednorazowe dodatki uzupełniające [4] zgodnie z równaniem zawartym w rozporządzeniu:

Jednak „różnica” (w prezentowanym przykładzie [1]: -63095,95, czyli 63095,95) nie jest równa sumie wyliczonych „z tej różnicy” jednorazowych dodatków uzupełniających ([2]: 63095,83); w tym przypadku obie kwoty różnią się o 12 groszy.

Dlaczego?

Wyjaśnienie faktyczne nie jest zupełnie proste, ale można rzecz wyjaśnić obrazowo w sposób następujący: wyobraźmy sobie, że oto w danej grupie awansu zawodowego jest 100 nauczycieli; wyobraźmy sobie, że w wyniku analizy wydatków na wynagrodzenia nauczycieli wyszła różnica (ujemna) = - 100,36 (minus sto złotych i trzydzieści sześć groszy); czyli należy dla nauczycieli w tej grupie policzyć jednorazowe dodatki uzupełniające…; załóżmy, że każdy z tych stu nauczycieli ma taką samą osobistą stawkę wynagrodzenia zasadniczego (równą na przykład 32172,63 zł), w proporcji do której ma być wyliczony ów jednorazowy dodatek uzupełniający; czyli – z racji równych wartości osobistych stawek wynagrodzenia zasadniczego – owe 100,36 zł różnicy należy podzielić na 100 równych części (bo jest 100 nauczycieli); czyli każdy otrzyma 1,00 zł…

…a jak podzielić na równe 100 części 36 groszy?

…to co zrobić – zostawić tak, jak jest na przykładowym tu wyżej rysunku, czy też może „z ręki dopisać” (w tym przypadku lub w innym „z ręki ująć”) „po grosiczku” dowolnie wybranym trzydziestu sześciu nauczycielom…?

Napiszę nie do końca poprawnie i elegancko: kilka lat temu „poziom nieświadomości” opisywanej tu kwestii (i wielu innych) był tak duży, że po pierwsze lepiej było o tym nie mówić, a po drugie – lepiej było po tym „grosiczku” tu i ówdzie zmienić; dziś „poziom świadomości” jest już na tyle duży, że chyba dla mocno zdecydowanej większości jest wiadomym, że prawdopodobieństwo tego, że wskazywane wyżej owe dwie kwoty będą sobie się równać („co do grosza”) – jest bardzo małe (dla 100 nauczycieli: 2%). Takich „niuansów”, których lepiej nie eksponować jest w analizie wydatków na wynagrodzenia nauczycieli znacznie więcej...

Teraz napiszę poprawnie: należy tak zrobić, aby było dobrze… - zalecana Aplikacja „liczy dobrze”…

Rzecz, której nie umiem rzetelnie wytłumaczyć: …jak tu z podziału liczby ujemnej wychodzą liczby dodatnie? Można to tłumaczyć na trzy możliwe następujące sposoby:
(1) …bo tak…
(2) …bo MEN tak chce…
(3) …bo to cud jest…
Proszę, dokonując analizy wydatków na wynagrodzenia nauczycieli, pozostawać w spokoju i dobrym usposobieniu – to taka coroczna (noworoczna) zabawa dla Wybranych…

Krzysztof Sługocki, 05.01.2019